KI Nuller Observation Description
The Keck Interferometer Nuller (KIN) is designed to detect faint mid-infrared emission located from tens to a few hundreds of milliarcseconds from a bright central star. The light from the star is suppressed by creating a destructive interference fringe along the Keck-Keck 85 meter baseline with the central null positioned on the star. The strongly variable mid-infrared background is removed using interferometric phase chopping along a short (~5 m) baseline created by dividing the Keck apertures into two components. KIN was designed primarily to detect the faint glow of a massive analog of the Sun's Zodiacal dust disk around a nearby star (more details), but it is potentially well suited to a broad range of astrophysical problems.
The science observations are made by taking observations with the central narrow dark fringe on the star (the "null" measurement) and with the central bright fringe on the star (the "peak" measurement), and finding the ratio of the light detected in these two states. This ratio, called the "null leakage", is directly related to the visibility amplitude. It can be represented as the sum of terms due to the astrophysical source and to the instrument. The astrophysical term would vanish if the star were a perfect point source, and is easily calculated for the case of a uniform disk photosphere which is small compared to the 25 mas spacing of the narrow fringes. For example, a star with a 1 mas diameter would produce an astrophysical leakage of N ~ 0.012. For a uniform source which is large compared to 25 mas, but smaller than ~600 mas (FWHM) field of view (which is not perfectly symmetric due to the split Keck aperture), the leakage contribution is approximately half of the total light from the extended source. If the extended emission is asymmetric, the fraction of light detected in the leakage will depend on the hour angle, as the interferometer transmission pattern will rotate with the project baseline rotation.
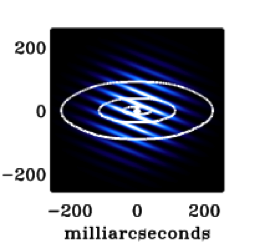 |
Schematic of the fringe pattern of the long baseline with the null on the central star. See Koresko et al 2006 for a more detailed view of the long and short baseline fringes during the nulling measurement phases. |
The measured fringe is dispersed over the N band with 20 channels from 8 to 13 microns. The null leakage is measured nearly independently in each spectral channel, and may be averaged across channels if desired. The best SNR occurs at the shortest wavelengths, and the longest wavelength channels are useful only for very bright stars.
The basic data product for a nulling experiment is the null leakage and the fundamental performance metric of the KIN is the uncertainty in the null leakage after calibration. In the approximation when the leakage is much smaller than 1, the observed raw leakage is the sum of a series of terms, some due to the astrophysical source and others due to imperfections of the instrument. The most important instrumental terms have to do with phase and amplitude errors, alignment errors (shear, rotation), and wavefront errors. If we neglect any potential complications having to do with the short baseline, and treat it as a simple modulator of the whole astronomical source, then the leakage is directly related to the traditional fringe visibility measured on the long baselines as
N = (1-V)/(1+V)
where N is the null leakage and V is the standard visibility amplitude.
The data reduction is performed in two stages, referred to as Level-1 and Level-2. The first consists of internal calibrations, i.e., those which rely on data taken on only a single star, and produces the total null leakage. The second step relies on observations of calibrator stars with known sizes to measure and subtract the instrumental contribution to this leakage. The residual signal, as a fraction of the stellar flux, after both stages of calibration is referred to as the calibrated leakage. The current calibrated leakage uncertainty is available on the nulling sensitivity page.
The precise control of the instrument to minimize the null leakage results in a good measurement of the visibility. Inverting the above equation yields
V = (1-N)/(1+N)
and the equivalent uncertainty in the squared visibility (the normal data product from visibility data) is
sigma_V2 ~ 4 * sigma_N.
For example, a null leakage uncertainty of 0.5% corresponds to a squared visibility uncertainty of 2%. This property means that the nulling observing mode is also suitable for N band observation programs even if a deep null is not needed to detect the extended emission.
In addition to the N band nulling data, K band fringe tracking data is also archived and the standard visibility data products are produced.
Helpful references
- Current nulling sensitivities and observation parameters
- Nulling at the Keck Interferometer, M. Colavita et al, 2006, SPIE v. 6268.
- Measuring Extended Structure in Stars using the Keck Interferometer Nuller, C. Koresko et al, 2006, SPIE v. 6268
Last updated July 31, 2007 - RLA
