The visibility is the
fundamental observable of the KI in the
operational mode refered to as "visibility amplitude"
(a.k.a. "visibility squared" or V2 mode). As explained in the
references and tutorials given in our basic
bibliography list, an interferometer measures
discrete components of the spatial frequency spectrum of the observed
object's brightness distribution on the sky. This spatial spectrum is
often called the "visibility function", a complex function in the
general case. The spatial frequencies sampled are a function of the
locations of the interferometer's apertures, the location of the
source in the sky, and the wavelength of observation.
When observing from the
ground, the phase of the
spatial spectrum is corrupted by atmospheric turbulence,
and is not recoverable using closure
phase techniques for a two-telescope
interferometer, such as the KI. Therefore, the useful
observable is the modulus of the spatial spectrum. Also, with only two
apertures, the KI can only obtain a relatively sparse sampling of
spatial frequencies
for a given object. Therefore, imaging by Fourier-inversion techniques
(common in radio-interferometry) is not
possible.
Nevertheless, an
optical interferometer such as the KI can offer important
advantages over a
conventional telescope. This is because the visibility amplitudes
measured correspond to the very
high spatial resolution given by the large
relatively separation between the apertures (or baseline length);
analogous to the
resolving power of a conventional telescope being given by the aperture
diameter. As an approximate rule, the maximum spatial frequency sampled
by an interferometer may be estimated as s(max)=B/wavelength; where B
is the length of the baseline vector projected on the sky. At 2.2
microns, and for B=85m, we have s(max)=187 cycles/arcsec. Similarly, a
convenient "angular resolution" definition is given by wavelength/B; or
5 milliarcsec for the example chosen above.
Experimentally, an
interferometer measures components of the visibility
function by forming interference fringes between the apertures. The
contrast and phase of these fringes
give the
amplitude and phase of the visibility function, respectively. In
practice, the
square of the visibility amplitude is often
measured, hence the nomenclature for the mode. In reality, the
atmosphere and
instrument degrade the ideal measurement, in a way that can be easily
calibrated using measurements of
targets of known visibility, such as stars known to appear as point
sources or stars of well known angular diameter.
Following standard practice in optical interferometry (and contrary to
the case of radio-interferometry), in
the KI data processing the
visibility is measured relative to the mean
flux detected. With such normalization, a
calibrated visibility of 1.0 is obtained for an object that is
unresolved by the KI (a point source), and a
visibility of 0.0 would be measured for an object that is completely
resolved. For partially resolved sources, a
visibility between 0.0 and 1.0 is measured.
Once raw KI visibilities have
been measured and calibrated, the
astrophysical information about theobject being studied can be
extracted using a priori knowledge and model
fitting techniques.
Let's consider some simple
examples. In Figure 1 we represent an object
on the sky that has a Gaussian brightness distribution. Note its
very small
angular extent, with a full-width at
half-maximum of 1
mas.
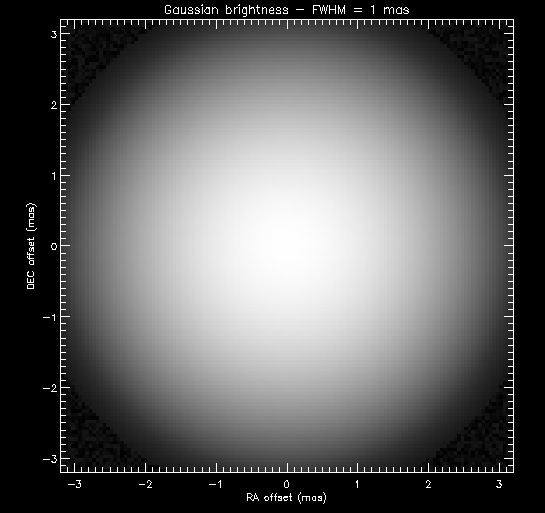
Figure 1. A simple object
represented by
a Gaussian brightness.
The spatial spectrum of the
Gaussian object, or visibility function, is
given by the 2D Fourier transform of the sky brightness. The visibility
amplitudes (squared) are shown in Figure
2. Overplotted, we show the track of spatial frequencies that
would be sampled by the KI if this object were
located at a declination of 20 degrees, and observed for an hour angle
range of -3 hr -> +3 hr. The time
sampling corresponds to a realistic KI data acquisition rate of 3
calibrated scans/hour. If you would like to learn how to calculate the
(u,v) spatial frequencies that would be sampled by a given
interferometer and given the source coordinates, please consult e.g.
the Thompson, Moran & Swenson reference in our bibliography. Note also that our
observations planning tool getCal makes
this computation for you.
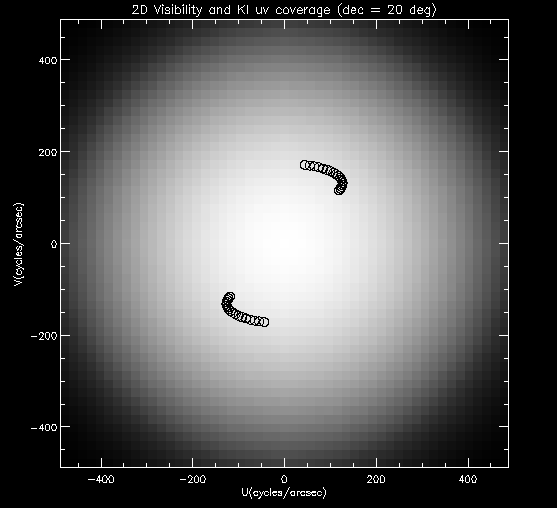
Figure 2. The 2D visibility (squared) map of the Gaussian brightness. The superposed
arcs show a realistic KI sampling of spatial frequencies.
Finally, Figure 3 shows the
visibility amplitude curve for this object,
along with the samples that KI would measure on this object. Since the
object is circularly symmetric
on the sky, its Fourier transform is also circularly symmetric and in
the top panel we represent the
visibilities as a function of the modulus of the spatial frequency
(u,v) pairs. To further illustrate the
geometry, in the bottom panel the visibilities are plotted
as a function of the projected baseline position angle. As the Earth
rotates the projected baseline may change
not only in orientation but also in length, hence even though our
source is circularly symmetric, there
are small visibility variations seen in the bottom plot.
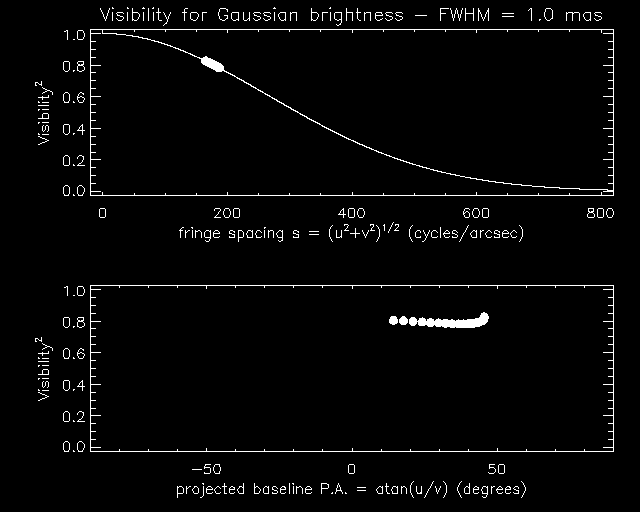
Figure 3. Gaussian source visibility curves and simulated KI samples.
Another simple example is shown
in Figure 4. This time we consider a
binary stellar system, where the
separation between the stars is only 5 mas. This object is not circularly symmetric, and therefore the visibilities measured will depend strongly on the relative orientation of the baseline vector and, in this case, the binary separation vector. Equivalent to baseline position angle, we now show the visibilities as a function of time, or source hour angle, and it can been seen how as the Earth rotates the visibilities trace the sinusoidal response characteristic of a binary system. Note that this variation would take place even if the projected baseline length remained constant over this time interval. As in the previous example, the samples that KI would measure are overplotted, and have been calculated assuming the same source declination and (realistic) sampling intervals.
separation between the stars is only 5 mas. This object is not circularly symmetric, and therefore the visibilities measured will depend strongly on the relative orientation of the baseline vector and, in this case, the binary separation vector. Equivalent to baseline position angle, we now show the visibilities as a function of time, or source hour angle, and it can been seen how as the Earth rotates the visibilities trace the sinusoidal response characteristic of a binary system. Note that this variation would take place even if the projected baseline length remained constant over this time interval. As in the previous example, the samples that KI would measure are overplotted, and have been calculated assuming the same source declination and (realistic) sampling intervals.
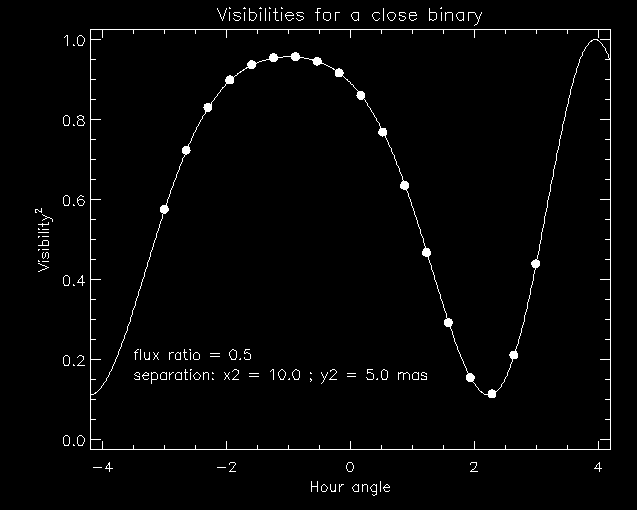
Figure 4. Visibility curve for a binary star and simulated KI samples.